中学３年数学練習問題　三平方の定理/空間図形への利用(1)

ＴＯＰ
＞
中学３年　数学　練習問題一覧
＞
三平方の定理／空間図形への利用（１）

勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。

～　中学３年　数学　～

Lesson 44　　　三平方の定理／空間図形への利用（１）

第７章　三平方の定理

＜前：Ｌ４４- 空間図形への利用(1) の問題　　Ｌ４５- 空間図形への利用(2) の問題：次＞

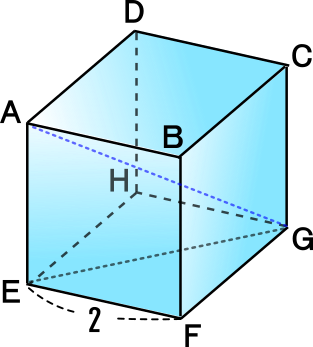
$三平方の定理$

【練習問題１】
右の図形の対角線の長さをそれぞれ求めなさい。
　　※長さの単位はｃｍとする

［１］　図形は立方体

　　＜ＥＧの長さを求める＞
　　　ＥＧ²＝ＥＦ²＋ＦＧ²なので、
　　　ＥＧ²＝２²＋２²
　　　　　＝８
　　　ＥＧ＝± $平方根$ ８
　　　　　＝±２ $平方根$ ２

　　　ｘ＞０なので、
　　　ＥＧ＝２ $平方根$ ２

　　＜ＡＧの長さを求める＞
　　　ＡＧ²＝ＡＥ²＋ＥＧ²なので、
　　　ＡＧ²＝２²＋（２ $平方根$ ２）²
　　　　　＝４＋８
　　　　　＝１２
　　　ＡＧ＝± $平方根$ １２
　　　　　＝±２ $平方根$ ３

　　　ｘ＞０なので、
　　　ＡＧ＝２ $平方根$ ３

　　≪答≫　２ $平方根$ ３ｃｍ

　　※別の解き方
　　　１辺がａｃｍの立方体の対角線の長さは、
　　　 $平方根$ ａ²＋ａ²＋ａ²
　　　＝ $平方根$ ３ａ²
　　　＝ $平方根$ ３ａ

　　　よって、１辺が２ｃｍの立方体の対角線の長さは、
　　　＝２ $平方根$ ３ｃｍ

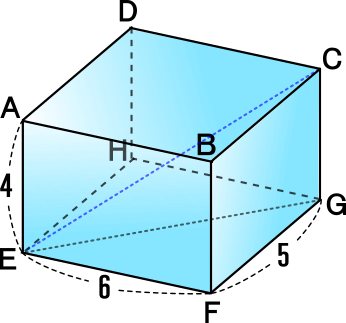
$三平方の定理$

［２］　図形は直方体

　　＜ＥＧの長さを求める＞
　　　ＥＧ²＝ＥＦ²＋ＦＧ²なので、
　　　ＥＧ²＝６²＋５²
　　　　　＝６１
　　　ＥＧ＝± $平方根$ ６１

　　　ｘ＞０なので、
　　　ＥＧ＝ $平方根$ ６１

　　＜ＣＥの長さを求める＞
　　　ＣＥ²＝ＣＧ²＋ＥＧ²なので、
　　　ＣＥ²＝４²＋ $平方根$ ６１²
　　　　　＝１６＋６１
　　　　　＝７７
　　　ＣＥ＝± $平方根$ ７７

　　　ｘ＞０なので、
　　　ＣＥ＝ $平方根$ ７７

　　≪答≫　 $平方根$ ７７ｃｍ

　　※別の解き方
　　　３辺の長さがａｃｍ，ｂｃｍ，ｃｃｍの直方体の対角線の長さは、
　　　 $平方根$ ａ²＋ｂ²＋ｃ²

　　　よって、１辺が４ｃｍ，５ｃｍ，６ｃｍ，の直方体の対角線の長さは、
　　　 $平方根$ ４²＋５²＋６²
　　　＝ $平方根$ １６＋２５＋３６
　　　＝ $平方根$ ７７ｃｍ

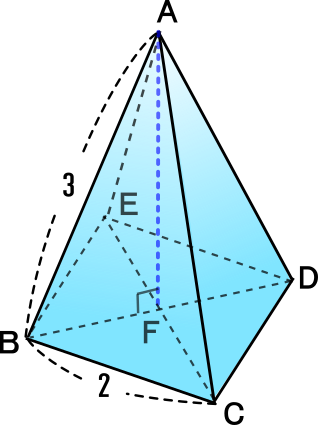
$三平方の定理$

【練習問題２】
右の正四角すいについて、以下質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　高さを求めなさい。

　　＜ＢＦの長さを求める＞
　　　ＢＦ²＋ＣＦ²＝ＢＣ²で、ＢＦ＝ＣＦなので、
　　　２ＢＦ²＝２²
　　　　ＢＦ²＝２
　　　ＢＦ＝± $平方根$ ２

　　　ｘ＞０なので、
　　　ＢＦ＝ $平方根$ ２

　　＜ＡＦの長さを求める＞
　　　ＢＦ²＋ＡＦ²＝ＡＢ²なので、
　　　 $平方根$ ２²＋ＡＦ²＝３²
　　　ＡＦ²＝７
　　　ＡＦ＝± $平方根$ ７

　　　ｘ＞０なので、
　　　ＡＦ＝ $平方根$ ７

　　≪答≫　 $平方根$ ７ｃｍ

［２］　体積を求めなさい。
　　　１３×２×２× $平方根$ ７
　　　＝４ $平方根$ ７３

　　≪答≫　４ $平方根$ ７３ｃｍ³

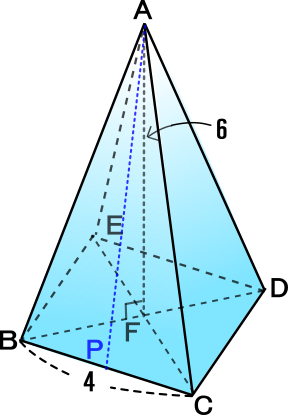
$三平方の定理$

【練習問題３】
右の正四角すいについて、以下質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　ＡＢの長さを求めなさい。

　　＜ＢＦの長さを求める＞
　　　ＢＦ²＋ＣＦ²＝ＢＣ²で、ＢＦ＝ＣＦなので、
　　　２ＢＦ²＝４²
　　　　ＢＦ²＝８
　　　　ＢＦ＝±２ $平方根$ ２

　　　ｘ＞０なので、
　　　ＢＦ＝２ $平方根$ ２

　　＜ＡＢの長さを求める＞
　　　ＡＢ²＝ＢＦ²＋ＡＦ²なので、
　　　ＡＢ²＝（２ $平方根$ ２）²＋６²
　　　ＡＢ²＝４４
　　　ＡＢ＝±２ $平方根$ １１

　　　ｘ＞０なので、
　　　ＡＢ＝２ $平方根$ １１

　　≪答≫　２ $平方根$ １１ｃｍ

［２］　表面積を求めなさい。

　　点ＡからＢＣに垂線をひき、ＢＣとの交点を点Ｐとする。
　　ＡＰは△ＡＢＣにおける高さとなる。

　　＜ＡＰの長さを求める＞
　　　ＡＰ²＋ＢＰ²＝ＡＢ²，ＢＰ＝４÷２＝２（ｃｍ）なので、
　　　ＡＰ²＋２²＝（２ $平方根$ １１）²
　　　ＡＰ²＝４０
　　　ＡＰ＝±２ $平方根$ １０

　　　ｘ＞０なので、
　　　ＡＰ＝２ $平方根$ １０

　　＜側面積を求める＞
　　　（４×２ $平方根$ １０÷２）×４
　　　＝１６ $平方根$ １０（ｃｍ²）

　　＜底面積を求める＞
　　　４×４＝１６（ｃｍ²）

　　＜表面積を求める＞
　　　（１６＋１６ $平方根$ １０）ｃｍ²

　　≪答≫　（１６＋１６ $平方根$ １０）ｃｍ²

$三平方の定理$

【練習問題４】
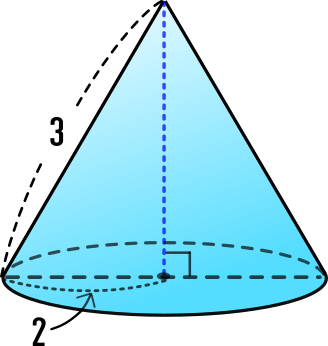
右の円すいについて、以下質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　高さを求めなさい。

　　　半径²＋高さ²＝母線²なので、
　　　２²＋高さ²＝３²
　　　高さ²＝５
　　　高さ＝± $平方根$ ５

　　　ｘ＞０なので、
　　　高さ＝ $平方根$ ５

　　≪答≫　 $平方根$ ５ｃｍ

［２］　体積を求めなさい。

　　　１３×π×２²× $平方根$ ５
　　　＝４ $平方根$ ５３π

　　≪答≫　４ $平方根$ ５３π ｃｍ³

$三平方の定理$

【練習問題５】
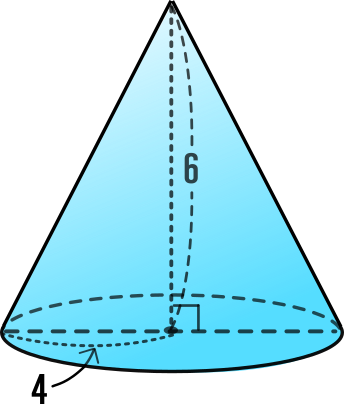
右の円すいについて、以下質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　母線の長さを求めなさい。

　　　母線²＝半径²＋高さ²なので、
　　　母線²＝４²＋６²
　　　母線²＝５２
　　　母線＝±２ $平方根$ １３

　　　ｘ＞０なので、
　　　母線＝２ $平方根$ １３

　　≪答≫　２ $平方根$ １３ｃｍ

［２］　表面積を求めなさい。

　　＜底面の円周（＝側面のおうぎ形の弧の長さ）＞
　　　２π×４＝８π

　　＜半径（母線）２ $平方根$ １３ｃｍの円の円周＞
　　　２π×２ $平方根$ １３＝４ $平方根$ １３π

　　＜側面積＞
　　　π×（２ $平方根$ １３）²×８π４ $平方根$ １３π
　　　＝５２π×２ $平方根$ １３
　　　＝１０４π $平方根$ １３

　　　有理化すると、
　　　１０４π× $平方根$ １３ $平方根$ １３× $平方根$ １３
　　　＝１０４ $平方根$ １３π１３
　　　＝８ $平方根$ １３π

　　＜底面積＞
　　　π×４²＝１６π

　　＜側面積＋底面積＞
　　　８ $平方根$ １３π＋１６π

　　≪答≫　（８ $平方根$ １３π＋１６π）ｃｍ²

　　※別の解き方
　　　円すいの表面積＝円周率×底面の円の半径×（母線＋底面の円の半径）でも計算できます。
　　　つまり、
　　　π×４（２ $平方根$ １３＋４）
　　　＝８ $平方根$ １３π＋１６π