中学生 勉強なんて 怖くない
～ 勉強が苦手な中学生のために ～
- ＴＯＰ
- ＞
- 中学３年 数学 練習問題一覧
- ＞
- 三平方の定理の基本
勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。
～ 中学３年 数学 ～
Lesson 41 三平方の定理の基本
第７章 三平方の定理
＜前：Ｌ４１- 三平方の定理の基本 の問題 Ｌ４２- 三平方の定理の平面図形への利用 の問題：次＞
【練習問題１】
以下のｘの長さを求めなさい。
※長さの単位はｃｍとする
[１]
三平方の定理より
１2＋１2＝ｘ2
ｘ2＝２
ｘ＝±
２
ｘ＞０なので、
ｘ＝２
≪答≫ ２ｃｍ
[２]
三平方の定理より
ｘ2＋６2＝１０2
ｘ2＝６４
ｘ＝±８
ｘ＞０なので、
ｘ＝８
≪答≫ ８ｃｍ
[３]
三平方の定理より
２2＋２2＝ｘ2
ｘ2＝８
ｘ＝±２２
ｘ＞０なので、
ｘ＝２２
≪答≫ ２２ ｃｍ
[４]
三平方の定理より
ｘ2＋４2＝６2
ｘ2＝２０
ｘ＝±２５
ｘ＞０なので、
ｘ＝２５
≪答≫ ２５ ｃｍ
【練習問題２】
以下のｘの長さを求めなさい。
※長さの単位はｃｍとする
[１]
三平方の定理より
２ 2＋３ 2＝ｘ2
ｘ2＝５
ｘ＝±５
ｘ＞０なので、
ｘ＝５
≪答≫ ５ ｃｍ
[２]
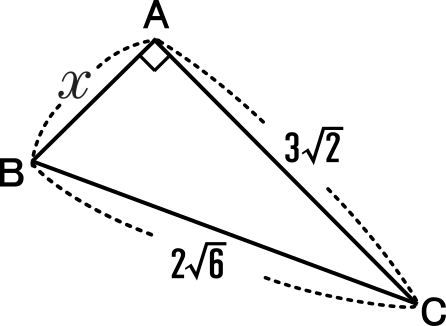
三平方の定理より
ｘ2＋（３２）2＝（２６）2
ｘ2＋１８＝２４
ｘ2＝６
ｘ＝±６
ｘ＞０なので、
ｘ＝６
≪答≫ ６ ｃｍ
[３]
三平方の定理より
（４２）2＋（４２）2＝ｘ2
３２＋３２＝ｘ2
ｘ2＝６４
ｘ＝±８
ｘ＞０なので、
ｘ＝８
≪答≫ ８ｃｍ
[４]
三平方の定理より
ｘ2＋（２３）2＝（４２）2
ｘ2＋１２＝３２
ｘ2＝２０
ｘ＝±２５
ｘ＞０なので、
ｘ＝２５
≪答≫ ２５ ｃｍ
【練習問題３】
以下の［ア］～［カ］は三角形の３辺それぞれの長さを示したものである。
この中から、直角三角形であるものをすべて選び、記号で答えなさい。
★印は、それぞれの３辺の中で一番長いので斜辺となる
［ア］ ２ｃｍ， ★４ｃｍ， ２３ｃｍ
２2＋（２３）2＝４2
４＋１２＝１６
１６＝１６
左辺と右辺が等しく、三平方の定理が成り立つので、直角三角形である
［イ］ ★６ｃｍ， ３３ｃｍ， ３ｃｍ
３2＋（３３）2＝６2
９＋２７＝３６
３６＝３６
左辺と右辺が等しく、三平方の定理が成り立つので、直角三角形である
［ウ］ ★４１３ｃｍ， ８ｃｍ， １２ｃｍ
８2＋１２2＝（４１３）2
６４＋１４４＝２０８
２０８＝２０８
左辺と右辺が等しく、三平方の定理が成り立つので、直角三角形である
［エ］ ４ｃｍ， ５ｃｍ， ★３５ｃｍ
４2＋５2＝（３５）2
１６＋２５＝４５
４１≠４５
左辺と右辺が等しくなく、三平方の定理が成り立たないので、直角三角形ではない
［オ］ ５ｃｍ， ３ｃｍ， ★２３ｃｍ
５ 2＋３ 2＝（２３）2
５＋３＝１２
８≠１２
左辺と右辺が等しくなく、三平方の定理が成り立たないので、直角三角形ではない
［カ］ ２２ｃｍ， ★４ｃｍ， ２２ｃｍ
（２２）2＋（２２）2＝４2
８＋８＝１６
１６＝１６
左辺と右辺が等しく、三平方の定理が成り立つので、直角三角形である
≪答≫ ア，イ，ウ，カ
【練習問題４】
以下の質問に答えなさい。
［１］ 直角三角形の斜辺が５ｃｍで残る２辺のうちの１辺が３ｃｍのとき、もう１辺の長さを求めなさい。
三平方の定理より
３2＋ｘ2＝５2
ｘ2＝１６
ｘ＝±４
ｘ＞０なので、
ｘ＝４
≪答≫ ４ｃｍ
［２］ 直角三角形の斜辺ではない２辺の長さがそれぞれ５ｃｍ， ７ｃｍのとき、斜辺の長さを求めなさい。
三平方の定理より
５ 2＋７ 2＝ｘ2
ｘ2＝１２
ｘ＝±２３
ｘ＞０なので、
ｘ＝２３
≪答≫ ２３ｃｍ
【練習問題５】
タクマ君は自分の家を出て直線で４００ｍ進み、交差点を直角に曲がってさらに直線で８００ｍ歩いてハルカさんの家に遊びに行った。
タクマ君の家とハルカさんの家の直線距離は何ｍか求めなさい。
三平方の定理より
４００2＋８００2＝ｘ2
１６００００＋６４００００＝ｘ2
ｘ2＝８０００００
ｘ2＝±４００５
※８０００００は数が大きいので、８０×１００００に分けて考える。
８０の平方根は４５、１００００の平方根は１００なので、
８０００００の平方根は、４５×１００＝４００５
ｘ＞０なので、
ｘ＝４００５
≪答≫ ４００５ ｍ
＜前：『第６章 円』の復習テスト の問題 Ｌ４２- 三平方の定理の平面図形への利用 の問題：次＞
中１数学・練習問題一覧 中２数学・練習問題一覧 中３数学・練習問題一覧
